EECinsights - Physics-based Domain Adaptation for Building Energy Forecasting
As part of the Physics-based Domain Adaptation project we are developing a framework to improve energy forecasting in buildings by incorporating mechanistic knowledge about energy behaviour with data-driven methods, in a domain adaptation (DA) schema. DA is an emerging subfield of Transfer Learning where knowledge is transferred and adapted across related domains. In our project we present a novel DA approach that leverages the generalizability innate in the governing structure of mechanistic models, namely linear time-invariant (LTI) state space models (SSM), to forecast for out-of-sample scenarios, related systems and longer timeframes beyond given building measurement data. We argue that by incorporating considerations of the governing structure in the modelling framework, we implicitly work towards global behaviour.
Our research is motivated by the following question:
What does the underlying structure of a building energy system look like and what governs it?
Any building energy system can be described as a dynamic system whose observed behaviour can be broken down into two main components: A) the dynamics of the heat transfer phenomenon (e.g., conduction, convection) and B) the influence of external factors (e.g., external ambient temperature). The core characteristics of an energy system are in fact governed by A and referred to as the state dynamics. We can think of the state dynamics as a mathematical vector field bound by the thermal states of the system. Thus, given a state space model, we can illustrate this vector field (left figure below) and quickly interpret how the dynamics behave in different state temperature scenarios, revealing the geometric structure of the global system in the process (right figure below). The geometry of the state space is governed entirely by the eigenvectors and eigenvalues of the state dynamics component. In thermal dynamics, the eigenvectors and eigenvalues represent the direction and rate of energy trajectories in the state space to reach thermal equilibrium.
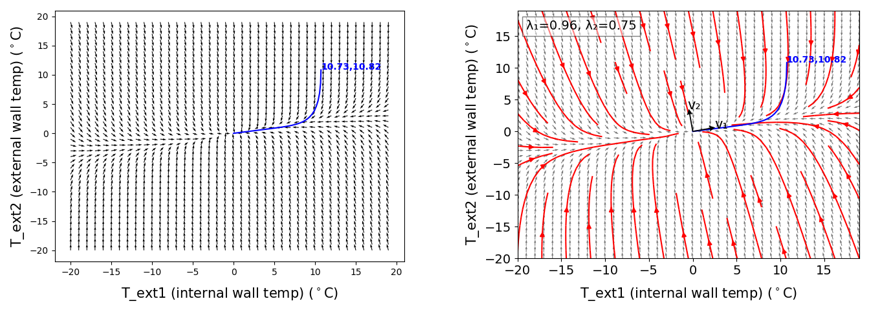
Can we leverage this geometric interpretation of governing structures to forecast beyond given measurement data?
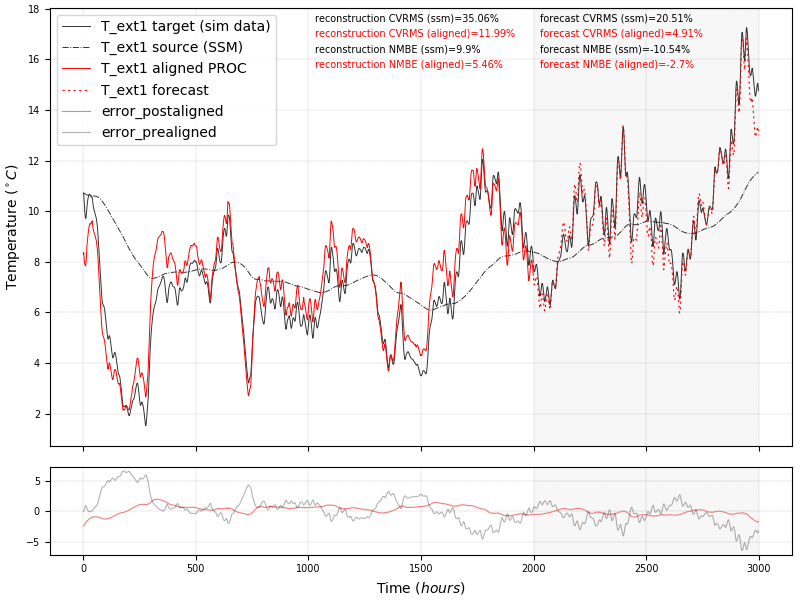
The notion of describing governing energy behaviour in buildings in terms of geometry motivated us to seek for geometric transformations between systems related by their similar physical phenomena. More specifically, in our Physics-based DA approach we seek for geometric transformation maps between the Physics-based mechanistic knowledge and measurement data via geometric alignment of their respective eigenvectors. The learned transformation is subsequently applied to transform fresh response data generated via the SSM to forecast beyond the available building measurement data, even for a different target system (undergoing similar phenomenon). The figure below illustrates an example application of our approach where we leverage the Physics-derived SSM of energy transfer through a wall, to forecast beyond (simulated) measurements of the internal surface temperature of a different but similar wall scenario.